ריבועים צבעוניים וליקויי חמה

המאמר מתאר את השיעורים שלי לתלמידי חטיבות ביניים - מלגות של הקרן הלאומית לילדים. הקרן מחפשת ילדים ונוער מחוננים במיוחד (מכיתה XNUMX ביסודי ועד תיכון) ומציעה "מלגות" לתלמידים נבחרים. עם זאת, הם אינם מורכבים כלל במשיכת מזומנים, אלא בטיפול מקיף לפיתוח כישרון, ככלל, לאורך שנים רבות. בניגוד לפרויקטים רבים אחרים מסוג זה, מדענים ידועים, אנשי תרבות, הומניסטים בולטים וחכמים אחרים, כמו גם כמה פוליטיקאים, מתייחסים ברצינות למחלקות הקרן.

פעילות הקרן משתרעת על כל המקצועות שהם מקצועות יסוד בבית הספר, למעט ספורט, לרבות אמנות. הקרן נוצרה ב-1983 כתרופה נגד המציאות דאז. כל אחד יכול לפנות לקרן (בדרך כלל דרך בית ספר, רצוי לפני תום שנת הלימודים), אבל יש כמובן מסננת מסוימת, הליך הסמכה מסוים.

כפי שכבר ציינתי, המאמר מבוסס על כיתות האמן שלי, במיוחד בגדיניה, במרץ 2016, בחטיבת הביניים ה-24 בתיכון III. חיל הים. במשך שנים רבות, סמינרים אלו אורגנו בחסות הקרן על ידי וויצ'ך תומלצ'יק, מורה לכריזמה יוצאת דופן ורמה אינטלקטואלית גבוהה. בשנת 2008 הוא נכנס לעשירייה הראשונה בפולין, שזכו לתואר פרופסור לפדגוגיה (הקבוע בחוק לפני שנים רבות). יש הגזמה קלה באמירה: "החינוך הוא ציר העולם".

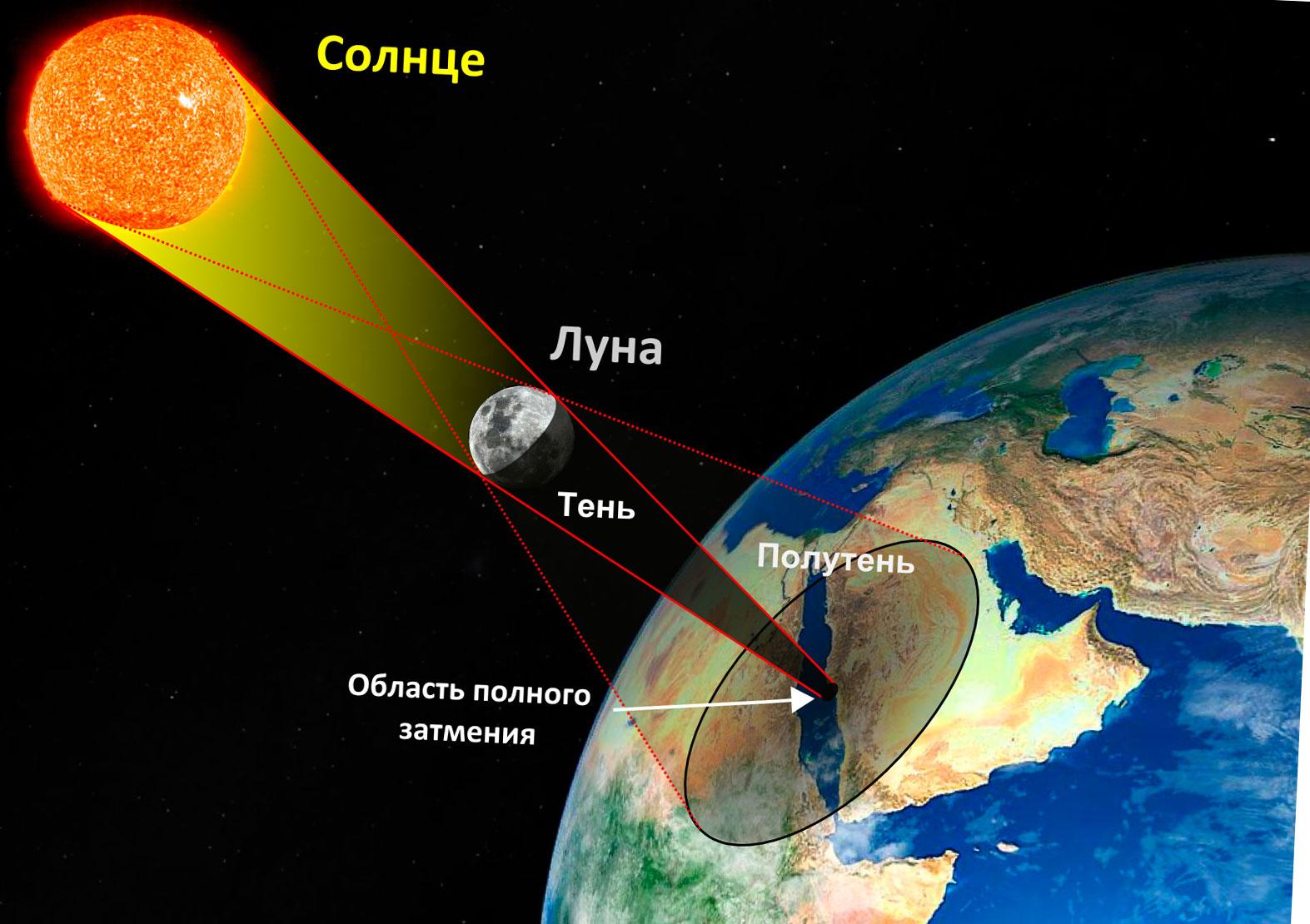
והירח הם תמיד מרתקים - אז אפשר להרגיש שאנחנו חיים על כוכב לכת זעיר בחלל ענק, שבו הכל בתנועה, נמדד בסנטימטרים ובשניות. זה אפילו קצת מפחיד אותי, גם נקודת המבט של הזמן. אנו למדים כי הליקוי המלא הבא, הנראה מאזור ורשה של היום, יהיה ב ... 2681. מעניין מי יראה את זה? הגדלים הנראים של השמש והירח בשמיים שלנו כמעט זהים - זו הסיבה שהליקויים כה קצרים וכל כך מרהיבים. במשך מאות שנים, דקות קצרות אלו אמורות להספיק לאסטרונומים לראות את קורונה השמש. זה מוזר שהם קורים פעמיים בשנה... אבל זה רק אומר שאיפשהו על פני כדור הארץ אפשר לראות אותם לפרק זמן קצר. כתוצאה מתנועות גאות ושפל, הירח מתרחק מכדור הארץ - בעוד 260 מיליון שנה הוא יהיה כל כך רחוק שאנחנו (אנחנו???) נראה רק ליקויים טבעתיים.

כנראה הראשון שניבא ליקוי חמה, היה תאלס ממילטוס (28-585 מאות לפני הספירה). כנראה שלא נדע אם זה אכן קרה, כלומר אם הוא חזה את זה, כי העובדה שהליקוי באסיה הקטנה התרחש במאי 567, 566 לפני הספירה היא עובדה מאושרת על ידי חישובים מודרניים. כמובן, אני מצטט נתונים לתיאור הזמן של היום. כשהייתי ילד, דמיינתי איך אנשים סופרים שנים. אז זה, למשל, XNUMX לפני הספירה, ערב השנה החדשה מגיע ואנשים צוהלים: רק XNUMX שנים לפני הספירה! כמה מאושרים הם בטח היו כשסוף סוף הגיע "העידן שלנו"! איזו תחלופה של אלפי שנים חווינו לפני כמה שנים!

המתמטיקה של חישוב תאריכים וטווחים ליקויים, אינו מסובך במיוחד, אלא עמוס בכל מיני גורמים הקשורים לסדירות, וחמור מכך, לתנועה הלא אחידה של הגוף במסלולים. אפילו הייתי רוצה לדעת את המתמטיקה הזו. כיצד יכול תאלס ממילטוס לבצע את החישובים הדרושים? התשובה פשוטה. חייבת להיות לך מפת שמיים. איך עושים מפה כזו? זה גם לא קשה, המצרים הקדמונים ידעו איך לעשות את זה. בחצות הלילה יוצאים שני כהנים אל גג המקדש. כל אחד מהם מתיישב ומצייר את מה שהוא רואה (כמו הקולגה שלו). אחרי אלפיים שנה, אנחנו יודעים הכל על תנועת כוכבי הלכת...

גיאומטריה יפה, או כיף על ה"שטיח"

היוונים לא אהבו מספרים, הם פנו לגיאומטריה. זה מה שנעשה. שֶׁלָנוּ ליקוי חמה הם יהיו פשוטים, צבעוניים, אבל מעניינים ואמיתיים לא פחות. אנו מקבלים את המוסכמה לפיה הדמות הכחולה נעה בצורה כזו שהיא מאפילה על האדומה. בואו נקרא לדמות הכחולה הירח, ולדמות האדומה שמש. אנו שואלים את עצמנו את השאלות הבאות:

1. כמה זמן נמשך ליקוי חמה;
2. כאשר חצי מהמטרה מכוסה;

   אורז. 1 "שטיח" רב צבעוני עם השמש והירח

3. מהו הכיסוי המקסימלי;
4. האם ניתן לנתח את התלות של כיסוי המגן בזמן? במאמר זה (אני מוגבל בכמות הטקסט) אתמקד בשאלה השנייה. מאחורי זה יש גיאומטריה נחמדה, אולי בלי חישובים משעממים. בואו נסתכל על איור. 1. האם ניתן להניח שזה יהיה קשור ל...ליקוי חמה?

אני חייב לומר בכנות שהמשימות בהן אדון ייבחרו במיוחד, מותאמות לידע ולכישורים של תלמידי חטיבות הביניים והתיכון. אבל אנחנו מתאמנים במשימות כמו מוזיקאים מנגנים סולמות, וספורטאים עושים תרגילי התפתחות כלליים. חוץ מזה, זה לא סתם שטיח יפה (איור 1)?

אורז. 2 ירח "כחול" ושמש "אדום".

הגופים השמימיים שלנו, לפחות בהתחלה, יהיו ריבועים צבעוניים. הירח כחול, השמש אדומה (הטוב ביותר לצביעה). עם ההווה ליקוי חמה הירח רודף אחרי השמש על פני השמים, משיג... וסוגר אותה. גם אצלנו זה יהיה אותו דבר. המקרה הפשוט ביותר, כאשר הירח נע ביחס לשמש, כפי שמוצג באיור. 2. ליקוי חמה מתחיל כאשר קצה דיסקת הירח נוגע בקצה דיסקת השמש (איור 2) ומסתיים כאשר הוא עובר מעבר לו.

אורז. 3 הירח מתקרב אל השמש באלכסון

אנו מניחים שה"ירח" זז תא אחד ליחידת זמן, למשל, לדקה. אז הליקוי נמשך שמונה יחידות זמן, נניח דקות. חֲצִי ליקוי חמה מעומעם לחלוטין מחצית החוגה סגורה פעמיים: לאחר 2 ו-6 דקות. גרף האחוזים הוא פשוט. במהלך שתי הדקות הראשונות, המגן נסגר באופן שווה בקצב של אפס עד 1, בשתי הדקות הבאות הוא נחשף באותו קצב.

הנה דוגמה מעניינת יותר (איור 3). הירח מתקרב אל השמש באלכסון. על פי הסכם התשלום לדקה שלנו, הליקוי נמשך 8√2 דקות - באמצע הזמן הזה יש לנו ליקוי מלא. הבה נחשב איזה חלק מהשמש מכוסה לאחר זמן t (איור 3). אם עברו t דקות מתחילת הליקוי, וכתוצאה מכך הירח הוא כפי שמוצג באיור. 5, אז (שימו לב!) לכן, הוא מכוסה (שטח ה-APQR הריבוע), שווה למחצית הדיסק הסולארי; לכן, הוא היה מכוסה כאשר, כלומר. לאחר 4 דקות (ואז 4 דקות לפני סוף הליקוי).

אורז. 4 גרף של פונקציית "הצללה".

מִכלוֹל נמשך רגע אחד (t = 4√2), והגרף של הפונקציה "חלק מוצל" מורכב משתי קשתות של פרבולות (איור 4).

הירח הכחול שלנו ייגע בפינה עם השמש האדומה, אך הוא יכסה אותה, לא הולך באלכסון, אלא מעט באלכסון. גיאומטריה מעניינת מופיעה כאשר אנו מסבכים מעט את התנועה (איור 6). כיוון התנועה הוא כעת וקטור [4,3], כלומר "ארבעה תאים ימינה, שלושה תאים למעלה". מיקום השמש הוא כזה שהליקוי מתחיל (מיקום A) כאשר הצדדים של "גרמי השמיים" מתכנסים לרבע מאורכם. כאשר הירח ינוע למיקום B, הוא יאפיל על שישית מהשמש, ובעמדה C הוא יאפיל לחצי. בעמדה D, יש לנו ליקוי מלא, ואז הכל חוזר אחורה, "כמו שהיה".

אורז. 5 חלק מהשמש מוסתר בזמן t

הליקוי מסתיים כשהירח נמצא בעמדה G. הוא נמשך כל עוד אורך חתך AG. אם, כמו קודם, ניקח כיחידת זמן את הזמן שבו הירח עובר "ריבוע אחד", אז אורך ה-AG שווה. אם נחזור למוסכמה הישנה לפיה גרמי השמים שלנו הם 4 על 4, התוצאה תהיה שונה (מה?). כפי שקל להראות, המטרה נסגרת לאחר t < 15. ניתן לראות את הגרף של פונקציית "אחוז כיסוי המסך" באיור. 6.

אורז. 6 גרף של הפונקציה "אחוז הגנה".

משוואת ליקוי וקפיצה

אורז. 7 חסימה של דיסק השמש במהלך הליקוי המוצג באיור. 6

בעיית הליקויים לא תהיה שלמה אם לא נתחשב במקרה של עיגולים. זה הרבה יותר מסובך, אבל בואו ננסה להבין מתי עיגול אחד מאפיל על חצי מהשני - ובמקרה הפשוט ביותר, כאשר אחד מהם נע לאורך הקוטר המחבר את שניהם. הציור מוכר לבעלי כרטיס אשראי כלשהו.

חישוב מיקום השדות הוא מסובך, מכיוון שהוא מצריך, ראשית, הכרת הנוסחה לשטח של קטע עגול, שנית, הכרת קשת הזווית, ושלישית (והגרוע מכל) היכולת לפתור משוואת קפיצה מסוימת. לא אסביר מהי "משוואה טרנזיטיבית", הבה נסתכל על דוגמה (איור 8).

אורז. 8 ליקוי חמה "כדורי".

חתך עגול הוא ה"קערה" שנשארת לאחר חיתוך עיגול בקו ישר. השטח של קטע כזה הוא S = 1/2r²(φ-sinφ), כאשר r הוא רדיוס המעגל, ו-φ היא הזווית המרכזית שעליה נשען הקטע (איור 8). זה מושג בקלות על ידי הפחתת שטח המשולש מאזור המגזר העגול.

פרק O₁O₂ (המרחק בין מרכזי המעגלים) שווה אז ל-2rcosφ/2, והגובה (רוחב, "קו המותניים") h = 2rsinφ/2. לכן, אם אנחנו רוצים לחשב מתי הירח יכסה חצי מהדיסק הסולארי, אנחנו צריכים לפתור את המשוואה: שלאחר הפישוט, הופכת:

אורז. 9 גרפים של שתי פונקציות

הפתרון של משוואות כאלה חורג מאלגברה פשוטה – המשוואה מכילה גם זוויות וגם פונקציות טריגונומטריות שלהן. המשוואה היא מעבר להישג ידן של שיטות מסורתיות. לכן זה נקרא לקפוץ. בואו נסתכל תחילה על הגרפים של שתי הפונקציות, כלומר פונקציות ופונקציות. נוכל לקרוא פתרון משוער מהאיור הזה. עם זאת, נוכל לקבל קירוב איטרטיבי או... להשתמש באפשרות פותר בגיליון האלקטרוני של Excel. כל תלמיד תיכון צריך להיות מסוגל לעשות זאת, כי זו המאה ה-20. השתמשתי בכלי Mathematica מתוחכם יותר והנה הפתרון שלנו עם XNUMX מקומות עשרוניים של דיוק מיותר:

SetPrecision[FindRoot[x==Sin[x]+Pi/2,{x,2}],20] {x⇒2.3098814600100574523}.

אורז. 10 אנימציה של ליקוי חמה ב-matematica

אנו הופכים את זה למעלות על ידי הכפלה ב-180/π. אנחנו מקבלים 132 מעלות, 20 דקות, 45 ורבע שנייה קשת. אנו מחשבים שהמרחק למרכז המעגל הוא O₁O₂ = רדיוס 0,808, ו"מותן" 2,310.